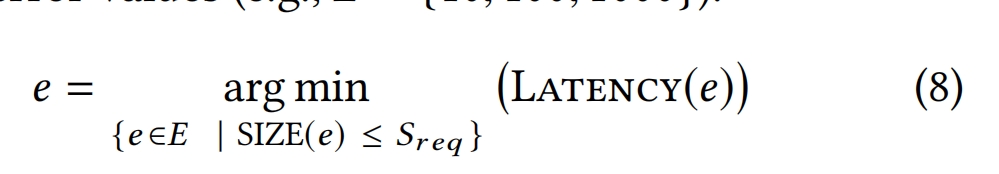Introduction
- 一种新的索引结构,它使用分段线性函数紧凑地捕捉数据中的趋势,并通过此减少索引的内存大小
- 这个索引结构的核心是一个参数error(查找key的预测position和实际position之间的最大距离)
- 为了实现查找性能和空间之间的trade-off,我们提出了一种cost model在给定查找延迟需求(eg 500ns)和存储预算(eg 100MB)的情况下帮助DBA选择合适的error参数
与最初的提出的技术相比,有以下优点:
(1)绑定最坏的查找性能
(2)有效地支持插入
(3)启动分页(所有数据不必驻留在一个连续的内存区域)
另一个有趣的点:
由于FITing-Tree的内部节点是树形结构,仍然可以应用前缀和后缀截断的技术来进一步减少索引的大小
OverView
Function Representation
使用分段线性函数拟合数据相比于更复杂的函数的优点
(分段线性函数近似的计算成本要低得多)
(1) 初始索引构建成本低
(2) 插入新的key延迟低
分段线性函数仍然存在误差error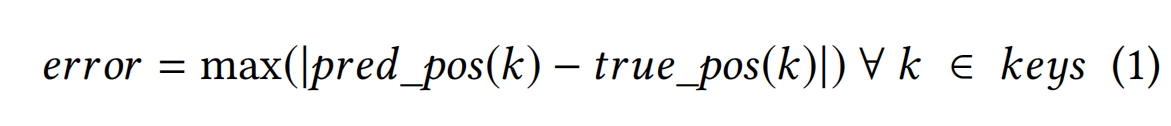
通过以上公式,我们可以定义一个segment(一组排序好的数据)
分割过程结束后,FITing-Tree将每个segment的边界和斜率存储在叶子节点中,减少了索引的总体内存占用
FITing-Tree Design
Clusted Indexes
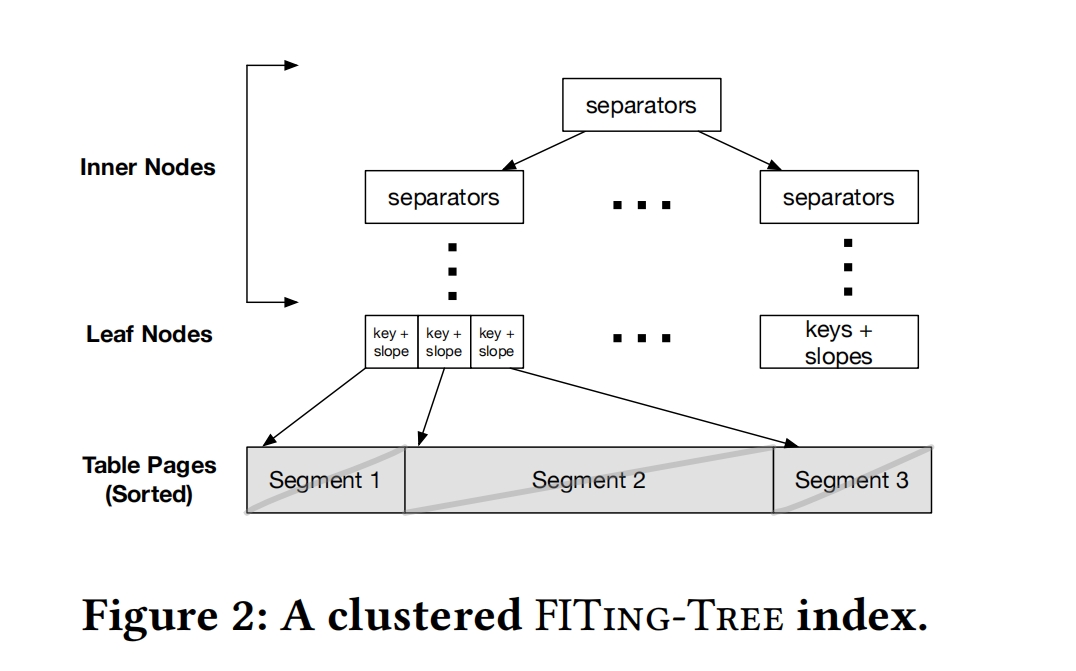
Non-clusted Indexes
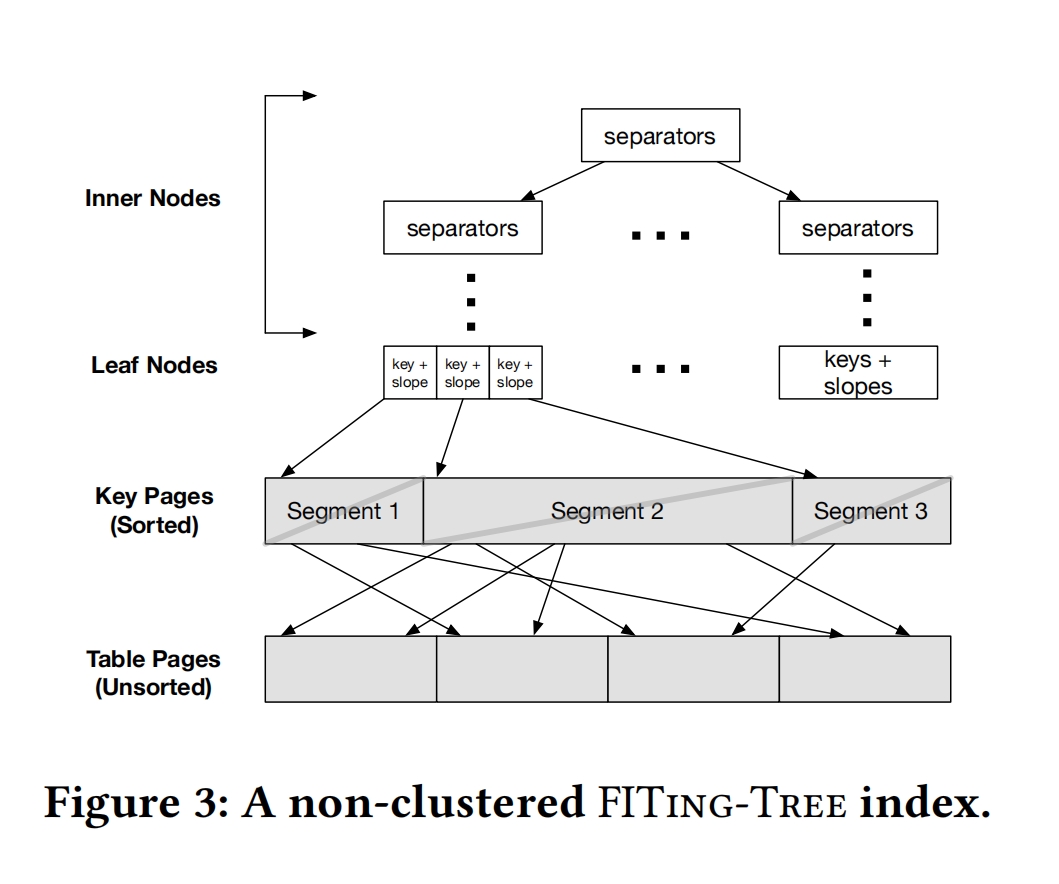
SEGMENTATION
Design Choices
下图是我们分段算法需要实现的目标,使得分段后满足最大的error
为了高效地构建索引和支持插入,需要一个高效地one-pass linear algorithm
Segment Definition
当一个segment添加一个key时,违反了这个max-error,则定义这个segment已经达到最大了
定理:最大segment所覆盖的最小位置数为max-error + 1
Segmentation Algorithm (思考: 可以不以用一个新的分段算法,或者在这个分段算法之上对这个进行改进)

如图5所示,说明了圆锥体的更新方式:点1时圆锥体的原点。点2更新了高斜坡和低斜坡。点3在原锥内,但是它只更新圆锥的上界(点3的小于下界之上的误差)。点4在更新锥的外部,因此将是新段的第一个点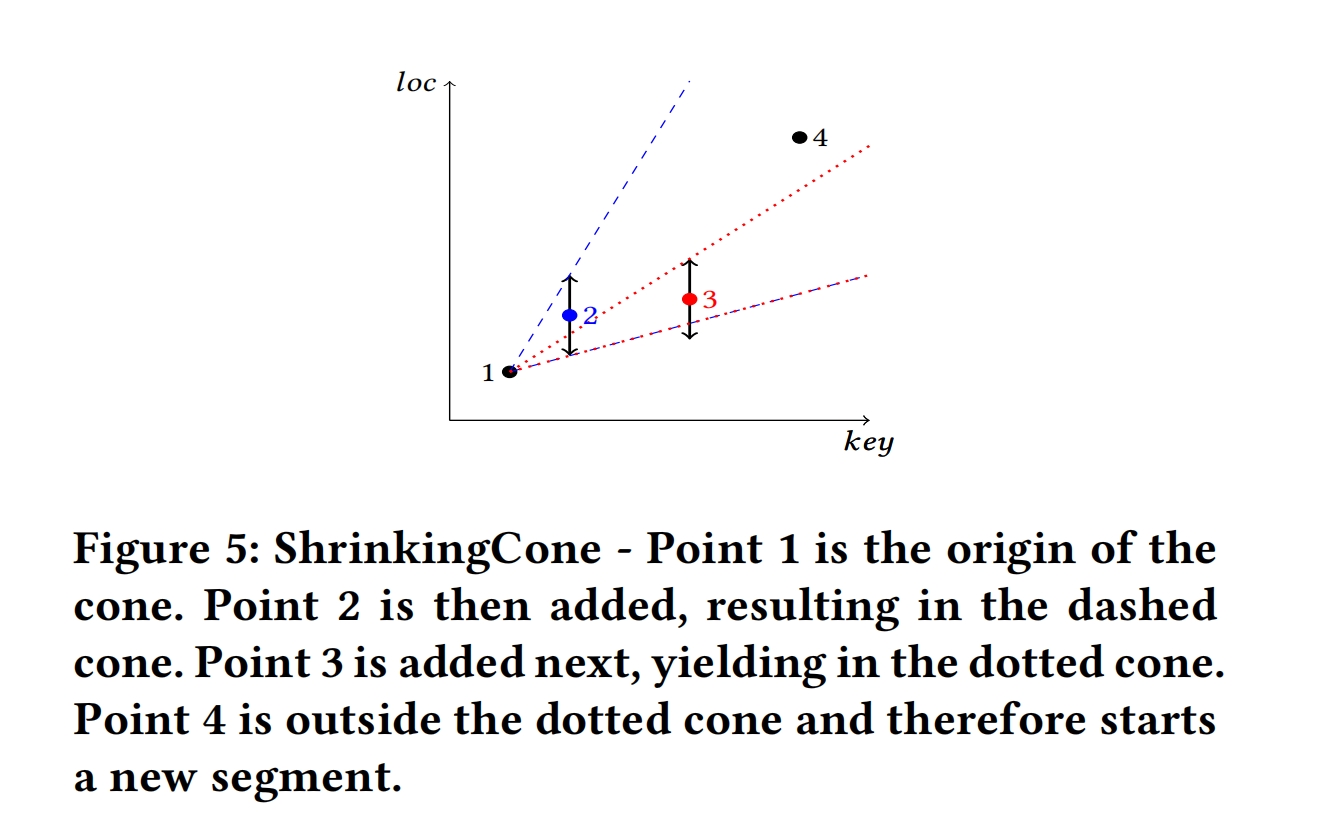
Algorithm Analysis
虽然以上收缩锥体算法的运行时间复杂度为O(n),但是它不是最优的。
INDEX LOOKUPS
Point Queries

Range Queries
INDEX INSERTS
In-place Insert Strategy
类似于页面的填充因子,我们将指定的误差分成两个部分:分割误差e和插入预算x
通过为每个segment保留插入预算x,可以确保插入新元素不会违反页面的错误
更具体地说,给定一个段,页面的总大小为|s| + 2*x(|s|为该段中的位置数,数据被放置在新页面的中间),在页面的开始和结束处产生x个空位置。在插入过程中如果所有的空白都被填满,那么就需要重新执行分割算法
Delta Insert Algorithm
- 就地插入策略的成本可能很高
- 为了减小插入时页面内数据移动的开销,每个segment包含一个额外的固定大小的缓冲区,此缓冲区保持排序,以实现有效的搜索和合并操作,一旦缓冲区达到预定的大小(buff),它与段中的数据进行合并,再次执行分割算法
- 另外,由于为每个段添加缓冲区可能违反FITing-Tree的max-error,我们透明地将缓冲区地大小合并到分割过程地错误阐述中,即分割过程中地错误阈值为(error -buff)

COST MODEL
由于指定的错误阈值error会影响查找和插入的性能以及索引的大小
提供cost model的目的就是帮助DBA在不同的工作负载下选择合适的错误阈值error
Latency Guarantee
查找延迟保证
由于查找需要找到相关的segment,然后搜索segment(数据+缓冲区),并且error的值会影响创建的段的数量(即更小的error会产生更多的段),我们使用一个函数,它返回为给定数据集创建的segment数量和error值。我们使用Se来表示指定数据集在给定错误阈值e下生成的segment的数量。
error值为e的总估计查找延迟可以用以下表达式来建模,其中b是tree的fanout,buff是segment的最大buffer大小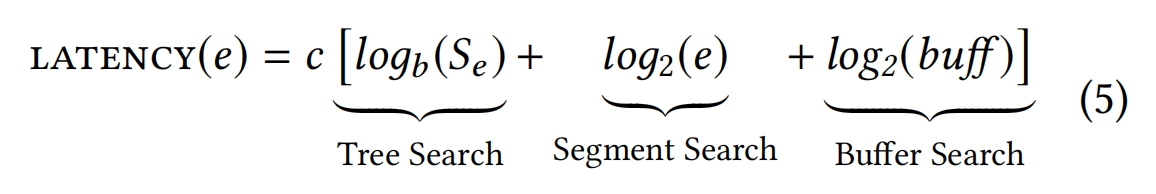
满足给定延迟要求并且存储占用最小的索引由以下表达式给出,其中E表示一组可能的错误值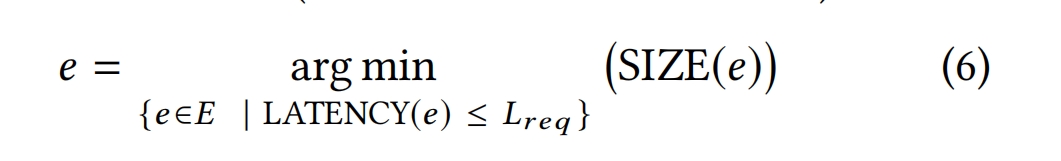
Space Budget
空间预算
可以用以下函数来估计给定的错误阈值e下的只读聚类索引的大小(byte)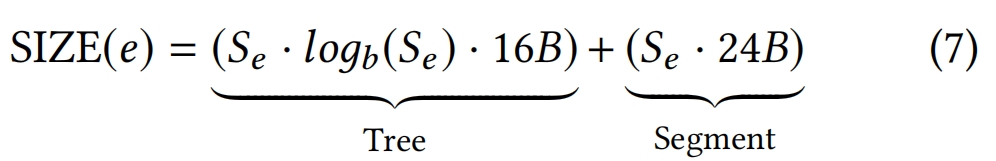
因此满足给定存储预算的最小误差阈值由以下表达式给出