背景和应用场景:
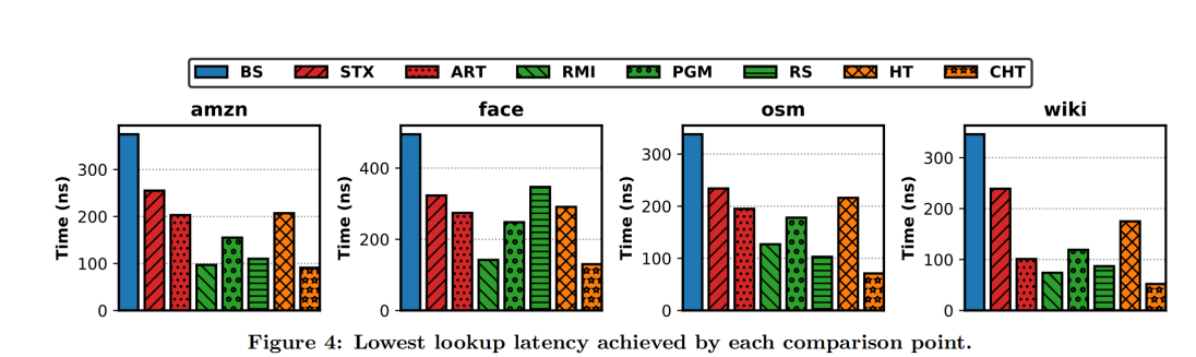
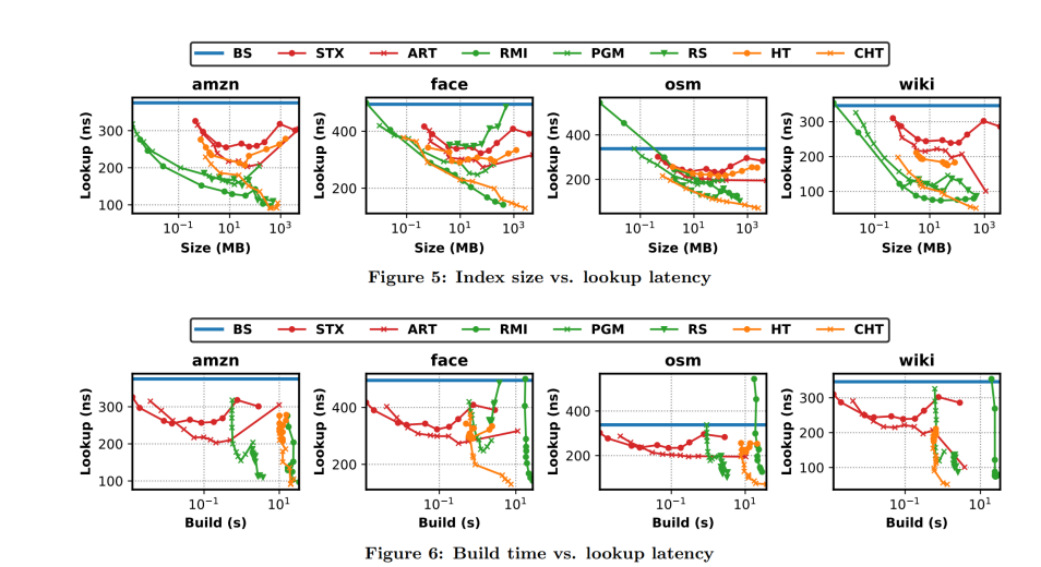
在之前的研究中,学习型索引的性能超过过了传统索引,这被归功于是利用数据分布这一特性。但是这篇文章认为,在比较试验中之学习型索引之所以能表现良好,是因为利用了一些隐含条件(例如,bulk-loading时,数据是排序的,数据的范围[min,max],…,))本文提出了一个传统索引结构(Hist-tree),利用了这些隐藏条件,并在只读工作负载的比较实验中,比RMI,PGM-index,RadixSpline的性能要好
问题描述:
学习索引做了一些隐含假设,例如
(1)假设bulk-loading数据已经排序
(2)数据的范围[min, max]
(3)数据是不被修改的
但是传统数据结构例如B-tree并没有这样的假设,这样会让B-tree的构建时间变得更长,或者导致B-tree和学习型索引进行比较实验时,处于劣势
方法:
Overview
提出Hist-tree(利用了隐含假设(1)(2))
以及压缩版本Compact-Hist-tree(利用了隐含假设(1)(2)(3))
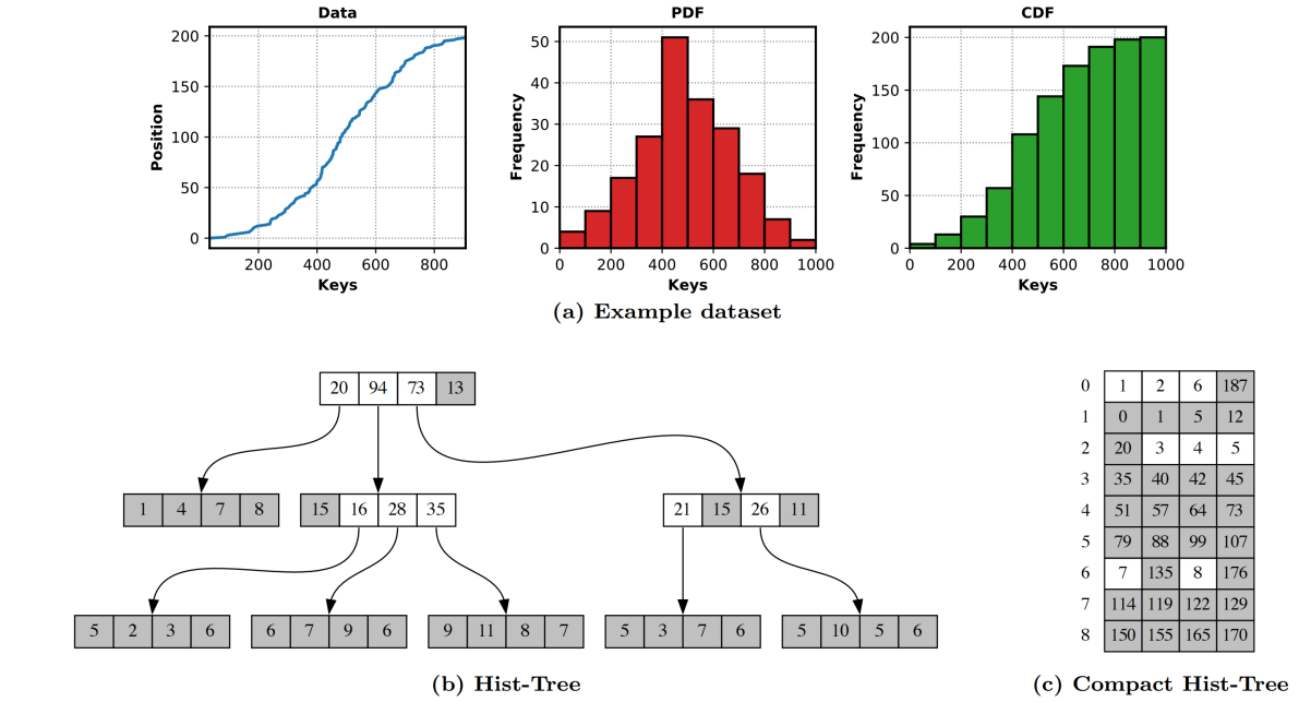
图中的Hist-tree是从一个数据集中选取200个key构建的,数据集的数据分布如(a)所示,(b)(c)为Hist-tree和Compact Hist-tree
(b)Hist-tree
每一个node根据histogram分成多个bin,terminal bin是灰色的,non-terminal bin是白色的,每个bin的值为该子树所包含的key的数量
查找过程为先锁定一个terminal-bin(有threshold),之后进行二分查找
(c) Compact Hist-tree
每一行代表一个node,每个node根据histogram分为多个binterminal bin是灰色的,non-terminal bin是白色的,白色的bin存储的值为child node的offset,灰色的bin存储累计直到该bin的所有key的数量
physical layout
Hist-tree的物理结构为两个32位整形数组,第一个数组包含的inner node(含有child node的node 或者说是 至少包含一个non-terminal bin的node),第二个数组包含leaf node(只有terminal bin的node)
例如:(b)中的root node要存储在第一个数组中占八个元素,其中由四个histogram bin计数组成,后跟四个child pointers(如果该pointer对应的bin为terminal bin或者指向leaf node,将高位flag标记为1),并且第一个和第四个child pointer的高位flag标记为1


结果: