最大流和最小割
最大流问题定义
找到一个从s出发,到t的流量最大的流
网络的流需要满足的条件
- 容量限制
- 流量守恒
如何找最大流
1.从流量为0开始,逐步增加流量
2.从s出发,找到一条道t的可行路径,并将流增加到这个路径能够支持的最大路径
3.在残存网络再找一条可行路径,增加相应的流
4.重复以上步骤
割的定义
将所有点划分为两个集合,这两个集合连接的边的集合称为割或者切
最小割定义
图是带权重的,划分的所有集合中,权重和最小的割
s-t最小割定义
划分的两个点的集合,必须是一个包含s,一个包含t
最大流和最小割定义
下面三个是等价的:
1.f是G的最大流
2.残存网络$G_f$找不到任何从s到t的新路径
3.s-t最小割和最大流是相等的
如何从残存网络找到一条从s到t的路径
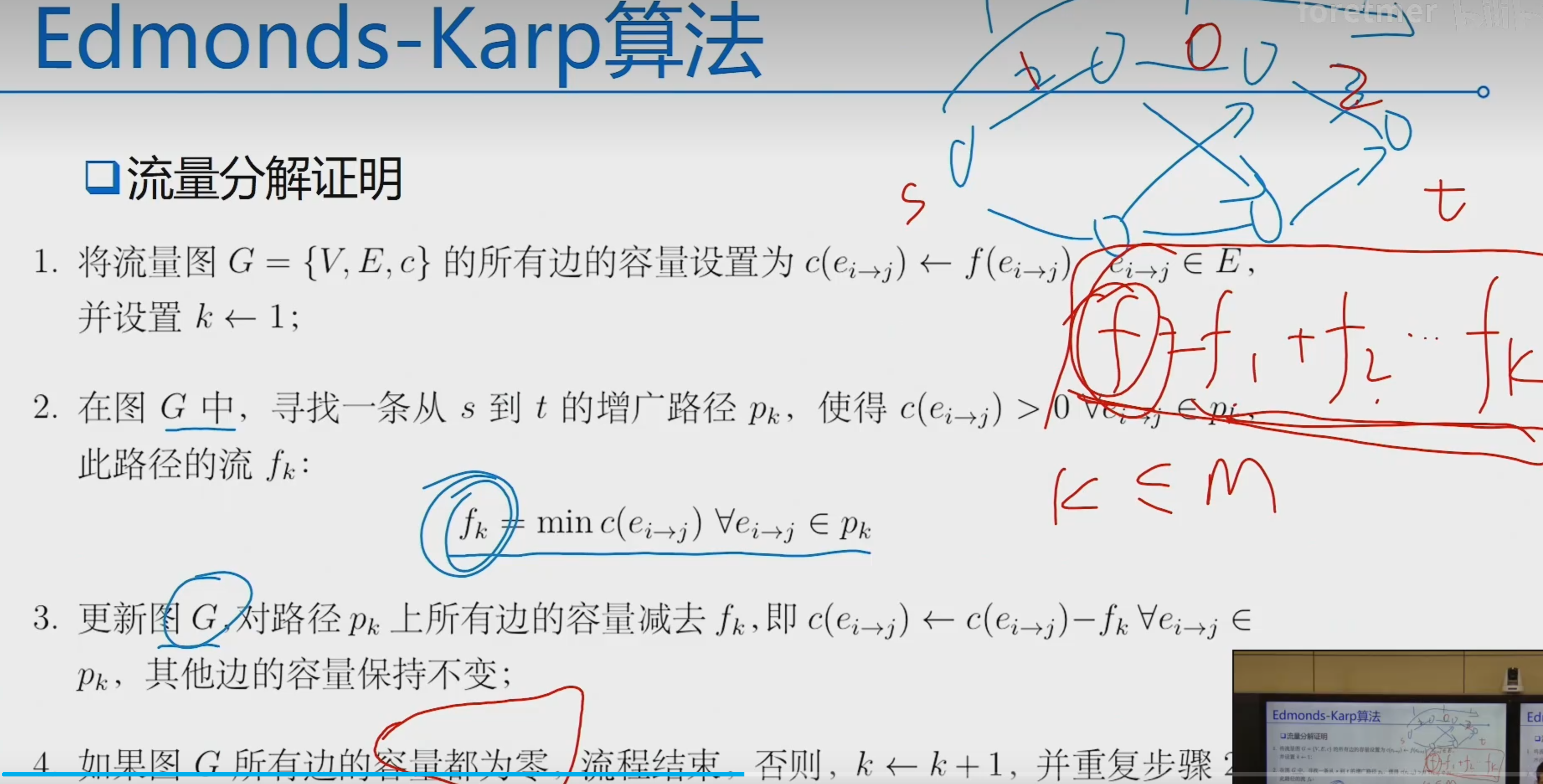
基于最短路径的Edmonds-Karp算法



基于最大容量路径的Edmonds-Karp算法
Dijkstra的改造
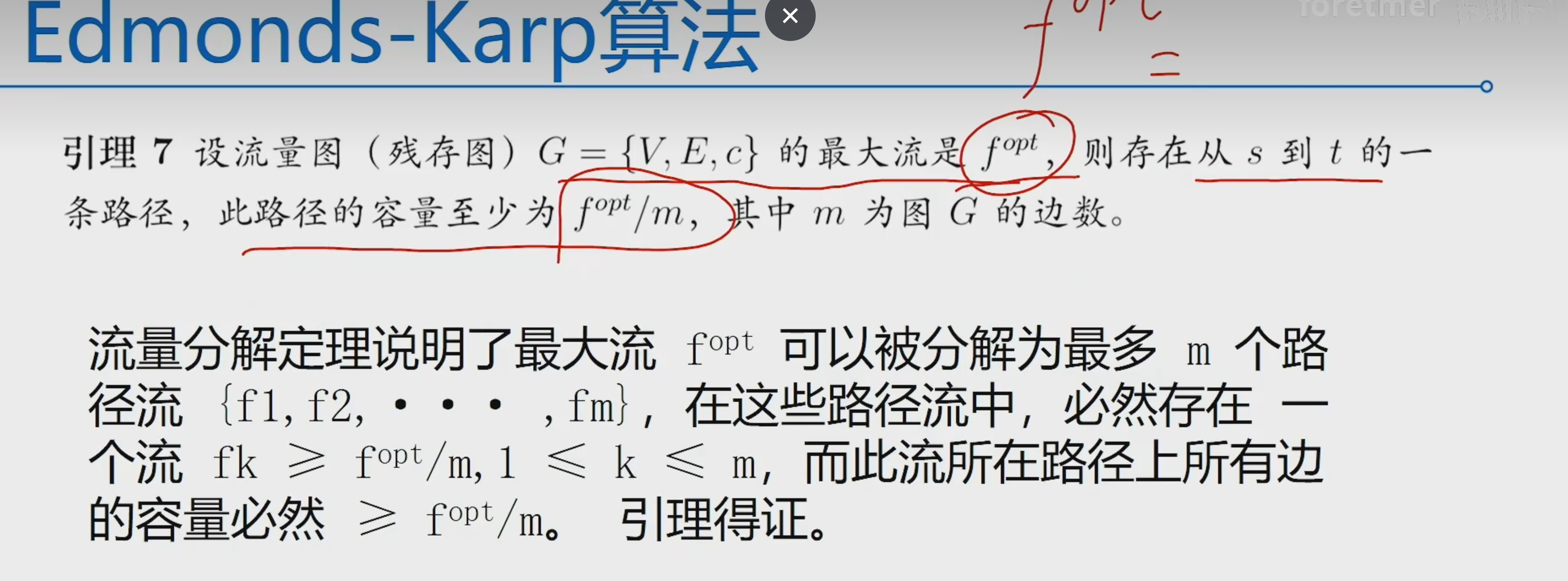
流量分解定理

图的中心性算法
度中心性DC
紧密中心性CC(Dangalchev变体)
中介中心性BC

快速中介中心性算法


特征向量中心性
PageRank
特征向量中心性算法的一个变体


社群发现算法
对网络进行社群划分的算法
基于模块度的算法
模块度
衡量社群划分好坏的一个指标,模块度的值越大,表示划分的越好
划分方式
1.合并方式
2.分割方式
LouVain算法待研究……
基于标签传播的算法


基于团的算法
团的定义:图的一个子图,其中任意顶点之间都有边连接,即团是一个完全子图
极大团的定义:如果一个团不包含在任何更大的团中,那么这个团称为极大团
最大团的定义: 顶点数最多的极大团
